Secured Deep Learning in Remote Devices

November 23, 2020 — Technical, Security, Deep Learning — 6 min read

In my previous article, we understood the basics of differential privacy. In this article, we will cover how differential privacy can be applied as Federated Learning that can be deployed in remote devices.

We'll be building a simple deep learning model to demonstrate the working of federated learning. As a prerequisite, you must have an intermediate level of understanding of Python and Deep Learning with the PyTorch library.

Introduction
What is Federated Learning?
How does Federated Learning work?
Installation
Implementation
Conclusion
Further Reading

Introduction

What is Federated Learning?

In Deep Learning, a problem of privacy arises with the centralization of the data used in training and development. The nature of data is for it to remain private, accessible only to the end-users, and not even to the organization that is providing the service. But in today's day and age, we are unsure if our privacy is ever at stake.

Any end-user device using deep learning sends the data to the cloud, the predictions/classifications are made, and it returns the results to the end-users. There is no guarantee that our data is secure. That’s where federated learning (Distributed deep learning), comes into the picture, to preserve privacy of the data.

By making the deep learning model distributed, we can solve the issue of privacy by running several independent deep learning models locally on each of the end-devices, and updating only their aggregated weights to the central deep learning model. This is federated learning in a nutshell.

For example, Google Assistant uses federated learning, when the deep learning model in our keyboard tries to predict the next word, by sending only the final aggregated model to the cloud. So, without uploading the details of any user to the cloud, we get the aggregated results based on local model training.

Image source

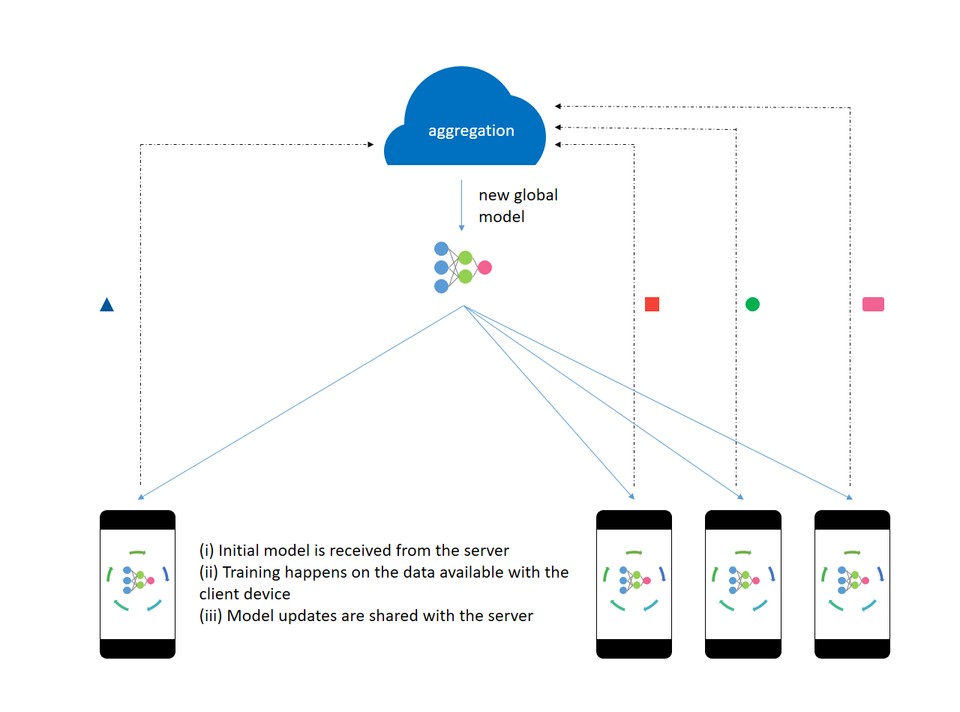
How does Federated Learning work?

Let's see an abstract overview of the working of federated learning.

1) The Server in the cloud gets initialized with a model/pre-trained model.

2) The Server sends a copy of the latest aggregated model to the request end-users’ device.

3) The local model gets trained locally, computes an update, and is sent back to the Global model.

4) The Server receives updates to the weights and averages them out by a weighting factor for each update in the training set from local.

5) Steps 1 - 4 are repeated for each request by the client devices.

This concept of Distributed deep learning has become very popular since 2017, after a blog post by Google AI. It has also been by Applethat they have been using it for Siri.

Having a better understanding of federated learning, let’s learn more about it, by implementing them.

Dataset description

In this tutorial, we are going to use the Boston housing dataset to predict the price of housing in Boston. The prediction is done based on various kinds of housing properties.

Installation

It's highly recommended to use Google Colab to get started right away. If you wish to run the below codes in your local system, download Anaconda by referring to the Anaconda documentation.

The libraries to be installed in Anaconda are:

Having installed all the above-mentioned libraries, it's time to get started with the implementation.

Importing libraries

If you are unsure of why these libraries are imported, you will understand them as you implement them further.

1import pickle
2import torch
3import torch.nn as nn
4import torch.nn.functional as F
5import torch.optim as optim
6from torch.utils.data import TensorDataset, DataLoader
7import time
8import copy
9import numpy as np
10import syft as sy
11from syft.frameworks.torch.fl import utils
12from syft.workers.websocket_client import WebsocketClientWorker

Parameters initialization

We set the parameters for the deep learning model, with the number of epochs as 100, learning rate as 0.001, and a batch size as 8 for every epoch. We also manually seed the random number generator.

1class Parser:
2  def __init__(self): # Constructor for initializing the parameters
3    self.epochs = 100 # Set Number of epochs to 100
4    self.lr = 0.001 # Set Learning rate to 0.001
5    self.test_batch_size = 8 # Set Batch size of Test dataset to 8
6    self.batch_size = 8 # Set Batch size of Train dataset to 8
7    self.log_interval = 10 # Set the time between data samples are taken
8    self.seed = 1 # Set a value for random number generator
9
10  args = Parser() # Call the class, to initialize the parameters
11  torch.manual_seed(args.seed) # Set the seed for random number generator to a fixed value

Loading the dataset

Pickling is the process whereby a Python object hierarchy is converted into a byte stream. Download this pickle file for the Boston Housing dataset.

This pickle file contains binary data for training the deep learning model.

On adding it to the path, we must open the file, and split both the training files and testing files, and convert them to Torch tensors for easier computations and compatibility with other PyTorch libraries.

A Torch tensor is a multi-dimensional matrix containing elements of a single data type. It's used as a data structure which helps make computation easier.

1with open('./boston_housing.pickle','rb') as f:
2  ((x, y), (x_test, y_test)) = pickle.load(f) # Load the file, and extract train and test files
3
4  x = torch.from_numpy(x).float() # Convert the train dataset numpy arrays to Torch tensors
5  y = torch.from_numpy(y).float()
6  x_test = torch.from_numpy(x_test).float() # Convert the test dataset numpy arrays to Torch tensors
7  y_test = torch.from_numpy(y_test).float()

Neural network architecture

We create a very simple neural network architecture consisting of 4 fully connected layers, with ReLU as activation functions used after each layer.

To understand more about Neural networks, read this article before further implementation.

ReLU is an activation function that converts the values below zero to zero, and the value remains the same if it is above zero.

This activation is highly preferred since, it doesn't activate all the neurons at the same time, during backpropagation, the weights are not updated.

1class Net(nn.Module): # Create a class containing Neural network architecture
2  def __init__(self): # Constructor to initialize the layers
3    super(Net, self).__init__() # Call the parent class, to inherit all attributes
4    self.fc1 = nn.Linear(13, 32) # Fully connected layer 1, of 13 input nodes and 32 output nodes
5    self.fc2 = nn.Linear(32, 24) # Fully connected layer 2, of 32 input nodes and 24 output nodes
6    self.fc4 = nn.Linear(24, 16) # Fully connected layer 3, of 24 input nodes and 16 output nodes
7    self.fc3 = nn.Linear(16, 1) # Fully connected layer 4, of 16 input nodes and 1 output nodes
8
9  def forward(self, x): # Method for Forward propagation
10    x = x.view(-1, 13) # Pass the transpose of the matrix of size 13 to FC1
11    x = F.relu(self.fc1(x)) # Activate the output of FC1
12    x = F.relu(self.fc2(x)) # Activate the output of FC2
13    x = F.relu(self.fc3(x)) # Activate the output of FC3
14    x = self.fc4(x) # The output of FC4 is returned
15    return x

Here, nn.Linear() creates a simple linear neural network layer of the specified input and output dimensions. Similarly, F.relu() accepts the fully-connected layer as an input, and returns the activated value.

Create workers for remote devices

To manage local end devices, we must bind the Torch tensors with the end-users using sy.TorchHook(torch). Since we aren't going to deploy them live on actual devices, we will assume virtual devices on different WebSocket ports.

Virtual workers are entities present on our local machine. They are used to model the behavior of actual workers. Then, we create 2 different workers for the demonstration.

1hook = sy.TorchHook(torch) # Bind the tensor with local workers
2end_device1 = sy.VirtualWorker(hook, id="device1") # 1st virtual entity
3end_device2 = sy.VirtualWorker(hook, id="device2") # 2nd virtual entity
4compute_nodes = [end_device1, end_device2] # List of workers

Distributing the training dataset to each worker

In this snippet, we separate the data and target values into two different lists. Then, we map the corresponding data and target values in the remote_dataset list for the respective iterated index.

1remote_dataset = (list(), list()) # Declare a tuple of lists
2train_distributed_dataset = [] # Declare a new list
3for batch_idx, (data,target) in enumerate(train_loader): # Load the data and target from the train dataset
4  data = data.send(compute_nodes[batch_idx % len(compute_nodes)]) # Separate the independent values from the train dataset
5  target = target.send(compute_nodes[batch_idx % len(compute_nodes)]) # Separate the target values from the train dataset
6  remote_dataset[batch_idx % len(compute_nodes)].append((data, target))

Here, batch_idx % len(compute_nodes) helps us index the remote_dataset. For our example, the index is 0 and 1.

Initializing neural networks for each remote device

We instantiate both the devices with separate neural network models. We also initialize optimizers for each of the neural networks.

Optimizers are algorithms or methods used to change the attributes of your neural network such as weights and learning rate to reduce the losses.

Here, we use the Stochastic Gradient Descent (SGD) optimizer. In short, SGD helps us reduce the loss faster, which happens batch-wise. More about SGD can be read this article.

1device1_model = Net() # Initialize neural network for Device1
2device2_model = Net() # Initialize neural network for Device2
3
4device1_optimizer = optim.SGD(device1_model.parameters(), lr=args.lr) # Initialize SGD optimizer for Device1
5device2_optimizer = optim.SGD(device2_model.parameters(), lr=args.lr) # Initialize SGD optimizer for Device2
6
7models = [device1_model, device2_model] # Make a list of models
8optimizers = [device1_optimizer, device2_optimizer] # Make list of optimizers
9
10model = Net()

Let's print out the initialized weights for both the models, to check if both the models get updated after federated learning aggregation. Here, we print out the weights of the last fully-connected layer fc3.

1device1_model.fc3.bias

Output:

1Out[1]:
2Parameter containing:
3tensor([-0.0842], requires_grad=True)

1device2_model.fc3.bias

Output:

1Out[2]:
2Parameter containing:
3tensor([-0.0982], requires_grad=True)

We see that device1 has a bias of -0.0842, and device2 has a bias of -0.0982.

Function for model training

On initializing all the models, we write functions to train the model and update the weights and losses. In update(), we predict the values based on input, calculate the losses, and backpropagate to improve the model. Here, for loss, we're using Mean Squared Error (MSE) loss function. In MSE, we find the mean squared difference between the predicted and expected value.

In train(), we iterate through each row, and update the weights and losses for each data, and return the aggregated values.

1def update(data, target, model, optimizer):
2  model.send(data.location)
3  optimizer.zero_grad() # Reset the optimizer
4  prediction = model(data) # Make predictions for the input data
5  loss = F.mse_loss(prediction.view(-1), target) # Calculate Mean Squared Error loss
6  loss.backward() # Backpropagate the values for training better
7  optimizer.step() # Step-up the optimizer for next iteration
8  return model
9
10def train(): # Function for training the model
11  for data_index in range(len(remote_dataset[0])-1): # For each row
12    for remote_index in range(len(compute_nodes)): # For each batch, within the data
13      data, target = remote_dataset[remote_index][data_index] # Extract the corresponding data and its target
14    models[remote_index] = update(data, target, models [remote_index], optimizers[remote_index]) # Update the weights and losses using optimizer
15
16  for model in models: # Iterate through each model
17    model.get() # Retrieve the parameters for the latest model
18
19  return utils.federated_avg({"device1": models[0],"device2": models[1]}) # Return the aggregated weights and losses of each device

Function for testing the model

This function helps us test the existing model, based on the test dataset, and returns the average loss for each data point.

1def test(federated_model):
2  federated_model.eval() # Sets the model to validation
3  test_loss = 0 # Initialize test loss to zero
4  for data, target in test_loader: # Iterate through each test data
5    output = federated_model(data) # Initiliaze the model for particular device
6    test_loss += F.mse_loss(output.view(-1), target, reduction='sum').item() # Compute the MSE loss
7    prediction = output.data.max(1, keepdim=True)[1]
8    test_loss /= len(test_loader.dataset)
9    print('Test set: Average loss: {:.4f}'.format(test_loss)) # Return the average loss

Updating the model in each remote device

For demonstration, we train and compute the predictions for each of the two devices. We print out the epoch number for training, and the time is taken to communicate with each end-device.

1for epoch in range(args.epochs):
2  start_time = time.time()
3  print(f"Epoch Number {epoch + 1}")
4  federated_model = train()
5  model = federated_model
6  test(federated_model)
7  total_time = time.time() - start_time
8  print('Communication time over the network', round(total_time, 2), 's\n')

Output:

1Out[3]:
2Epoch Number 1
3Test set: Average loss: 615.8278
4Communication time over the network 0.09 s
5Epoch Number 2
6Test set: Average loss: 613.6289
7Communication time over the network 0.07 s
8Epoch Number 3
9Test set: Average loss: 610.8525
10Communication time over the network 0.08 s
11......
12Epoch Number 98
13Test set: Average loss: 40.4832
14Communication time over the network 0.07 s
15Epoch Number 99
16Test set: Average loss: 40.2277
17Communication time over the network 0.07 s
18Epoch Number 100
19Test set: Average loss: 40.0887
20Communication time over the network 0.07 s

Now, let's check if the aggregated weights of both the devices have changed or not.

1device1_model.fc3.bias

Output:

1Out[4]:
2Parameter containing:
3tensor([1.3315], requires_grad=True)

1device2_model.fc3.bias

Output:

1Out[5]:
2Parameter containing:
3tensor([1.3244], requires_grad=True)

We see the bias for both the models have changed to 1.3315 and 1.3244 for device1 and device2 respectively. It can be inferred that both the models have been trained and the weights have been updated.

Conclusion

As there are no high-level APIs to remotely deploy the model onto the end devices, virtual devices were used to act as end devices. However, the virtual devices exhibited seamless deployment and communication to the global model.

The weights were updated perfectly in each of the remote devices, thus the overall accuracy of the model improved well. The ever-rising need for privacy and decentralization of data is met by the emergence of systems utilizing Differential Privacy.

The cost of computation has been nerfed due to the use of distributed systems and the deployment of machine learning and deep learning systems remotely on the cloud. Even devices that have low computation power can deploy powerful models at the client’s end.

Therefore, federated learning systems are highly effective in providing a highly secure and reliable abstraction of data, by capitalizing on the factors mentioned previously.

In conclusion, we now have a better understanding for the need of federated learning. We looked at an overview of how deep learning models preserve the privacy of data in deep learning for end-devices.

You can checkout the complete code here. We highly recommend reading and implementing a few examples to get a better understanding of federated learning.

To summarize:

We understood what federated learning is.
We got an insight into how it works.
We implemented federated learning for remote devices.

Secured Deep Learning in Remote Devices

Table of contents

Introduction

What is Federated Learning?

How does Federated Learning work?

Dataset description

Installation

Importing libraries

Parameters initialization

Loading the dataset

Neural network architecture

Create workers for remote devices

Distributing the training dataset to each worker

Initializing neural networks for each remote device

Function for model training

Function for testing the model

Updating the model in each remote device

Conclusion

Further Reading